Radiation Problems
Area of applications of QuickWave software for electromagnetic design and simulations.
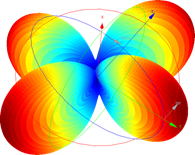
Radiation and scattering patterns calculations, in a form of 2D and 3D characteristics, including radiation parameters extraction, e.g. antenna gain, power radiated, radiation efficiency, axial ratio, etc., extraction of linear and circular polarisation components, calculation of radiation and scattering patterns in an arbitrary isotropic medium, etc.